Introduction
Differential privacy, as a technique to preserve privacy in the data collection process, is categorised into centralised differential privacy (CDP) and local differential privacy (LDP). CDP normally requires a trustworthy third party to collect and process the data before revealing the distribution of the data without compromising the information of each individual entry. This note is about two mechanisms that achieve CDP, the Laplace mechanism and exponential mechanism.
The Laplace mechanism
The Laplace mechanism is for queries of continuous data, i.e. “How many” questions. It adds noise to the numeric result (return_result = true_result + noise), such that adding or removing a single entry from the database does little effect on the result.
To achieve so, the noise can be set to obey the laplace distribution.
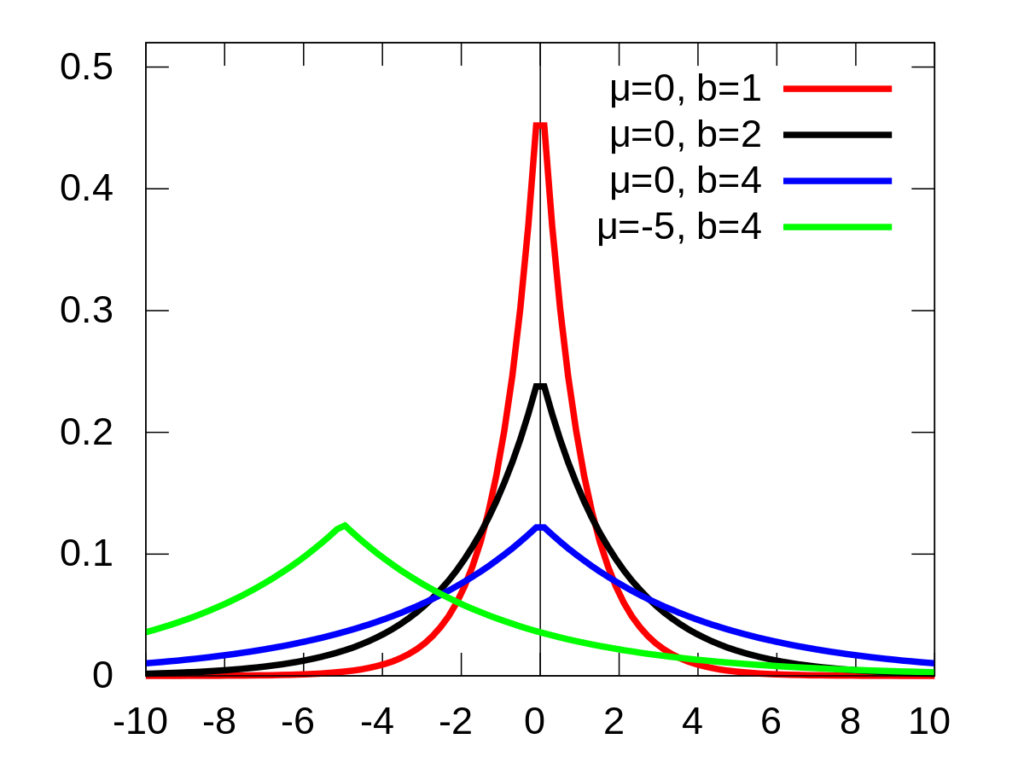
Looking at the three lines where µ=0, it means the noise has a large probability to approach 0, and small probability to be a large positive or negative number.
The parameter b equals to sensitivity/epsilon. Epsilon is the privacy budget in differential privacy. In short, larger epsilon leads to more precise result but lower privacy level, vice versa. Sensitivity is the maximum change that the change of a single entry can bring to the query result. For example, for queries regarding “the number of people”, the sensitivity is 1, because an additional entry of people can change the result by 1 at most.
The exponential mechanism
The exponential mechanism is for queries of discrete data, i.e. “what is” questions. This mechanism renders a probability of returning different results, rather than returning a certain result. For example, for the question “What is the colour that most people like”, if the true answer is red, the mechanism may have 90% chance returning red, 5% chance returning blue, 5% chance returning green, rather than returning red for sure.
