作者: Alan
2022.4.6-2022.4.19 旅行
希腊
圣托里尼
蓝顶教堂们



爱琴海的房子和看书的人





日落和我们






动物岛友会





半山




特色小商品



白色才属于爱琴海




爱琴海的餐食









雅典
卫城



宪法广场卫兵换岗仪式



雅典的甜品


意大利
罗马
斗兽场



万神殿



许愿池


沿途



罗马的餐食



梵蒂冈
外景



梵蒂冈博物馆









圣彼得大教堂




瑞士
苏黎世
街道



玫瑰池





卢塞恩
酒店








城景






美食




黄金列车上






格林德瓦
小镇




First山













施佩茨









法国
巴黎
罗浮宫




迪士尼


我们俩对上一次小朋友时期去香港迪士尼的记忆已经很模糊,她说很需要给大朋友的自己留下更清楚和新鲜的迪士尼体验。
冒着买不着票的风险排了一早上的队,还好我们挺幸运。






城市





区块链中的密码学:zk-SNARKs 概述 (英)
I am starting to learn and write about cryptography use cases in blockchain technology. I will skip the basic stuff like digital signature, public-key cryptography in general, and look into some specific technologies that are used in some specific cryptocurrencies projects.
I will start with zk-SNARKs in this one. zk-SNARKs stands for zero knowledge Succinct Non-interactive Argument of Knowledge. Zero-knowledge here is exactly the popular protocol in cryptography where a prover can verify that the prover knows certain knowledge to a verifier without revealing it. In cryptocurrencies, zk-SNARKs is a variant of zero knowledge proof that is able to verify a transaction to the nodes without revealing the information about this transaction. This is giving a nice privacy feature to the blockchain world where every transaction is normally publically available. Zcash is an example crypto project that uses zk-SNARKs.
Before going into the technical details, it is worth noticing that zero-knowledge is actually the focus of this protocol in terms of its construction, instead, most efforts of this protocol are on efficiency. Unlike traditional zero knowledge proof that requires frequent communication between the prover and the verifier, zk-SNARKs requires very little communication between the two parties since it is costly in the blockchain world.
So what do zk-SNARKs do exactly? Say Alice creates a transaction and wants to transfer 10 bitcoin to Bob. Alice would need to tell the whole world all about this transaction because the nodes need the information to check whether the transaction is valid. With zk-SNARKs, Alice can prove the transaction is valid without revealing the details of the transaction.
Let’s focus on hiding the amount of the transaction. How can a transaction be verified if the amount is not revealed? zk-SNARKs do so by providing proofs of:
1) the number of coins Alice has equals the number of coins she sends to Bob plus the number of the change (Bitcoin’s UXTO protocol requires all money to be spent in a transaction and the remaining part is the change).
2) the number of coins Alice going to spend is not negative.
3) Alice does have that amount of coins as input.
The first point can be achieved by homomorphic encryption without revealing the number. That is, E(a+b) = E(a) + E(b), where a and b are the money spent and the change. By applying an encryption function that is addition homomorphic, doing addition before encryption and doing encryption before addition outputs the same result, which means a and b do not need to be sent in plain text.
With the first point satisfied, an evil thing Alice can do is to send a negative number to Bob, which will also pass the test of addition. So Alice also needs to prove the number is not negative, in other words, the number is in a certain range. At a rather high level, the range proof needs to be expressed as some polynomials. This was a bit hard to understand for me and it totally worth another article to explain. In short, computable problems can be expressed in polynomials. The verifier can then check whether certain x values in the polynomials correspond to the correct y values. The reason for using polynomials is that, even one simple change in a factor in polynomial results in different y values in almost every corresponding x value, which means a single random check on a certain x value already gives a great guarantee of the correctness of the knowledge.
The last point is to prove that Alice does own that much money. The first method is to use the output from the previous transactions that Alice received as the input of this transaction. As we can imagine, we then have a problem of proving the very first transaction is valid without revealing the number, otherwise all efforts of handling later transactions would be in vain. This is again out of the range of this article unfortunately 🙂 The second method is to keep the so-called world state in the blockchain and the balance of Alice can be checked in the world state. Of course, the balances are hashed in the world state, it’s in the form of Merkle trees actually.
This article will stop here, leaving so many problems unexplained. How to transform the problem into polynomials? How is this protocol non-interactive? Hopefully I will write about them soon 🙂
七百年后
太WALL-E了这首歌

今年的英国生活
今年是被lockdown支配的一年,干得最多的呢就是在家里做吃的

还有做吃的

和做吃的

还有唱歌唱到被隔壁投诉
街上还是有很伦敦的艺术家们

就这样吧!明年再见!
保护隐私预防歧视的工作流
网站: http://thediscriminationfreemodel.uk
我的毕业设计是一个防止算法歧视的工作流. Demo和实验放在了网站上.
防止人工智能算法歧视的工作很多, 但很多研究提出的方法并不考虑用户隐私, 是基于有对训练集有控制权的假定提出的.
因此我设计了一个工作流, 通过可信第三方的介入, 只应用不需要访问训练集的方法, 帮助在公司用算法分类用户的过程中减少歧视.
其中还应用了差分隐私减少这个工作流对企业的影响. 本来为了防止歧视, 工作流的设计限制了企业对用户隐私数据的访问. 但是鉴于这些数据可以有其他商业用途, 应该给企业一定的访问权限. 差分隐私正好可以让企业在统计级别访问这些隐私数据, 而又不揭露个人隐私.
中心化差分隐私的Laplace机制和指数机制(英)
Introduction
Differential privacy, as a technique to preserve privacy in the data collection process, is categorised into centralised differential privacy (CDP) and local differential privacy (LDP). CDP normally requires a trustworthy third party to collect and process the data before revealing the distribution of the data without compromising the information of each individual entry. This note is about two mechanisms that achieve CDP, the Laplace mechanism and exponential mechanism.
The Laplace mechanism
The Laplace mechanism is for queries of continuous data, i.e. “How many” questions. It adds noise to the numeric result (return_result = true_result + noise), such that adding or removing a single entry from the database does little effect on the result.
To achieve so, the noise can be set to obey the laplace distribution.
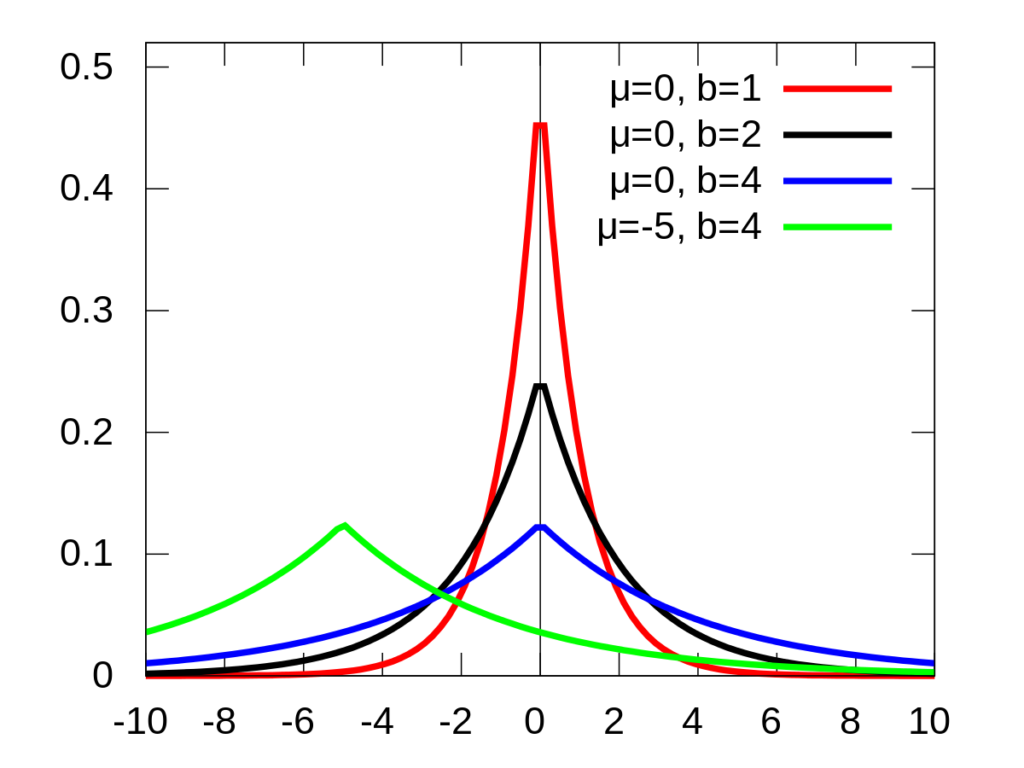
Looking at the three lines where µ=0, it means the noise has a large probability to approach 0, and small probability to be a large positive or negative number.
The parameter b equals to sensitivity/epsilon. Epsilon is the privacy budget in differential privacy. In short, larger epsilon leads to more precise result but lower privacy level, vice versa. Sensitivity is the maximum change that the change of a single entry can bring to the query result. For example, for queries regarding “the number of people”, the sensitivity is 1, because an additional entry of people can change the result by 1 at most.
The exponential mechanism
The exponential mechanism is for queries of discrete data, i.e. “what is” questions. This mechanism renders a probability of returning different results, rather than returning a certain result. For example, for the question “What is the colour that most people like”, if the true answer is red, the mechanism may have 90% chance returning red, 5% chance returning blue, 5% chance returning green, rather than returning red for sure.
